计算数值分析实验1--使用不同方法实现插值
不同方法插值算法实现已知插值节点序列(xi , yi),i = 0,1,2,……,n,用 Lagrange 插值多项式L n (x)计算的函数f (x)在点x0的近似值。123456789101112131415161718function b = lagrange( x,y,x0 )%实现拉格朗日插值汉书值的求解% 此处显示详细说明n = length(x);%总插值个数D = x0;p = 0.0;for k=1:n t = 1.0; for i = 1:n if i~=k t = t * (D-x(i))/(x(k)-x(i)); end end p = p+t*y(k);endb = p;%plot(D,p);end 已知插值节点序列(xi , yi),i = 0,1,2,…,n,用牛顿(Newton)插值值多项式N (x)n计算的函数f (x)在点0 x的近似值。123456789101112131415161718192021222324252627function...
Java实现多端图书管理系统
主要就是实现的程序模块化,实现了一个基本档案关系系统,并且有许多的账户可以注册,管理员可以修改其中的内容,有兴趣可以自己打开看看,文尾链接内饰我的代码,感兴趣可以看看,完全分享主要服务端代码如下: 1234567891011121314public Server() throws IOException{ InetAddress liushen = InetAddress.getLocalHost(); String s = liushen.getHostAddress(); System.out.println("地址嗷嗷嗷为:"+s); server = new ServerSocket( 12345, 100 ); int number=1; while(true){ displayMessage( "正在等待设备……\n" ); Socket connection = server.accept();...
MFC实现快乐连连看
...
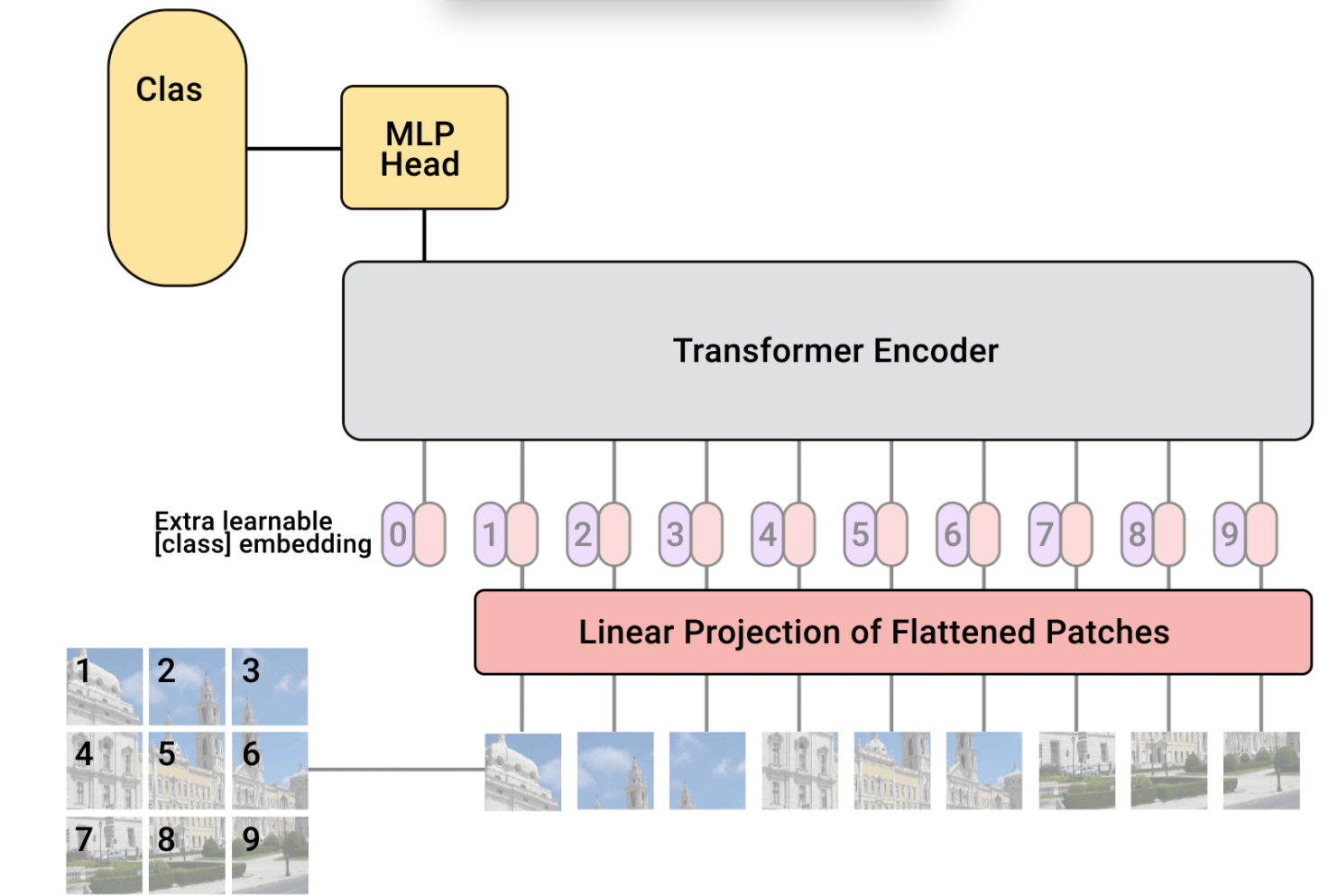
CNN+transformer入门学习
本文章将讲解从机器学习开始后的主要算法,以时间为线
计算机数值分析笔记
计算机数值分析章节:首先就是我们的插值方法,这一章讲的是如何将一组离散的点,进行处理,形成一个函数的值,主要重点是拉格朗日余项定理,拉格朗日插值,牛顿插值,还有一些简单的抛物线性插值等等,就是利用待定系数法,主要就是学习插值的基函数,系数和余项。 其次就是数值积分的相关内容,这里有简单的抛物线积分,矩形积分,梯形积分等问题。背公式就行,注意其中的许多对称性,考前看那些例题就可以 再常微分方程是指有一些式子带有导数之类的,没办法给他转换为正常的y = f(x)的形式,导致后面的计算非常困难,这一节就是把他的计算简单化,通过固定公式转化为一堆离散的点,这样就很容易求解了。 再就是方程求根的迭代法,这里建议直接背公式,很容易理解。 最后线性方程组的数值解法主要靠的是迭代和直接两种方法,直接你也会,主要就是迭代,要注意他的收敛性 下面是资源区,里面有我考试的考纲和我的笔记插值方法 数值积分 常微分方程 方程求根的迭代法 线性方程组的解法
机器学习笔记
机器学习-machine learning | ML 定义:机器学习是一种特殊的算法,不是某个特定的算法,能够让计算机在数据中学习从而进行预测。所以,机器学习不是某种具体的算法,而是很多算法的总称。机器学习包含了很多种不同的算法,深度学习就是其中之一,其他方法包括决策树,聚类,贝叶斯等。深度学习的灵感来自大脑的结构和功能,即许多神经元的互连。人工神经网络(ANN)是模拟大脑生物结构的算法。不管是机器学习还是深度学习,都属于人工智能(AI)的范畴。所以人工智能、机器学习、深度学习可以用下面的图来表示: 基本思路:(1).把现实生活中的问题抽象成数学模型,并且很清楚模型中不同参数的作用(2).利用数学方法对这个数学模型进行求解,从而解决现实生活中的问题(3).评估这个数学模型,是否真正地解决了现实生活中的问题,解决的如何最后就会发现,不是所有问题都可以转换成数学问题的。那些没有办法转换的现实问题 AI...